What are Sets?

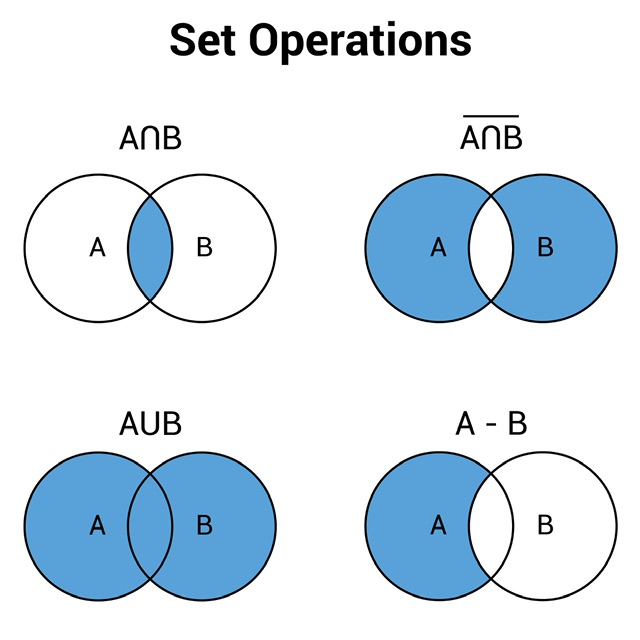
A set is defined as a collection of distinct objects, called elements, that are considered a single entity. These elements can be anything, such as numbers, letters, people, or even other sets. A set is defined by its elements, and not by how they are represented or described. For example, the set {1, 2, 3} is the same as the set {3, 1, 2}, and both represent the set of the first three positive integers. Sets are an important tool in mathematics and other fields, such as computer science and statistics, for modeling and analyzing various phenomena. They are used to define and study relations between objects, as well as to define operations such as union, intersection, and complement, which are useful in many areas of mathematics and beyond.

Types of Sets

There are several types of sets in mathematics, each with its unique properties and characteristics. Some common types of sets include:

Finite sets

A set that has a definite number of elements is called a finite set. For example, the set of the first five positive integers {1, 2, 3, 4, 5} is finite.

Infinite set

A set that has an infinite number of elements is called an infinite set. For example, the set of all positive integers {1, 2, 3, ...} is infinite.

Empty set

A set with no elements is called an empty set. It is denoted by the symbol ∅ or {}. It is also known as the null set.

Singleton set

A set that includes exactly one element is a singleton set. For example, {2} is a singleton set. The smallest odd number forms a singleton set.

Subset

A set  A is said to be a subset of a set B if every element of A is also an element of B. The subset relationship is denoted by the symbol ⊆. For example, {2, 3} is a subset of {1, 2, 3}.

Superset

A set B is said to be a superset of a set A if every element of A is also an element of B. The superset relationship is denoted by the symbol ⊇. For example, {1, 2, 3} is a superset of {2, 3}.

Power set

The power set of a set A is the set of all subsets of A. It is denoted by P(A). For example, the power set of {1, 2} is {{}, {1}, {2}, {1, 2}}.

Disjoint sets

Two sets A and B are said to be disjoint if they have no elements in common. For example, {1, 2} and {3, 4} are disjoint sets.

Equal sets

Two sets A and B are said to be equal if they have the same elements. For example, {1, 2} and {2, 1} are equal sets.

Set Operations

There are five major operations of sets. These are:

Union of Sets

The union of two sets P and Q is the set that contains all the elements that are in either P or Q or both. The union of P and Q is denoted as P ∪ Q.

For example, if P = {1, 2, 3} and Q = {2, 4, 6}, then P ∪ Q = {1, 2, 3, 4, 6}.

Intersection of Sets

The intersection of two sets P and Q is the set that contains all the elements that are in both P and Q. The intersection of P and Q is denoted as P∩ Q.

For example, if P = {1, 2, 3} and Q = {2, 4, 6}, then P∩ Q = {2}.

Difference of Sets

The difference between the two sets P and Q is the set that contains all the elements that are in P but not in Q. The difference between P and Q  is denoted as P\Q.

For example, if P = {1, 2, 3} and Q = {2, 4, 6}, then P \ Q = {1, 3}.

Complement of Set

The complement of a set P is the set of all elements that are not in P. The complement of P is denoted as P'.

For example, if P = {1, 2, 3} and the universal set is U = {1, 2, 3, 4, 5}, then P' = {4, 5}.

Cartesian product of Sets

The Cartesian product of two sets P and Q is the set of all ordered pairs (a, b) where a is an element of P and b is an element of Q. The Cartesian product of P and Q is denoted as P × Q.

For example, if P = {a, b} and Q= {c, d}, then P × Q = {(a, c), (a, d), (b, c), (b, d)}.

Graphical representation Of Sets: Venn diagrams

Venn diagrams are graphical representations used to illustrate relationships between sets. They are named after John Venn, a British mathematician. A Venn diagram consists of one or more overlapping circles, each representing a set. The area inside a circle represents the elements that belong to that set, and the area outside the circle represents the elements that do not belong to the set. The overlap between two or more circles represents the elements that belong to both or all of the sets.

Venn diagrams can be used to visualize various set operations, such as union, intersection, and complement. They can also be used to solve problems involving set theory and logic.

Conclusion

Sets are an important tool in mathematics and have a wide range of applications in both pure and applied mathematics. Sets provide a concise and clear way to represent collections of objects or numbers. They allow us to group objects or numbers based on common properties, which is useful for many mathematical applications.

Frequently Asked Questions

Q1. What are Bounded Sets?

A set is said to be bounded if there exist numbers A and B such that every element of the set has an absolute value (or magnitude) that is less than or equal to A, and greater than or equal to B. In other words, a bounded set is limited in size and contained within some specified range.

For example, consider the set S = {x | -1 ≤ x ≤ 1}, which is the set of all real numbers that are greater than or equal to -1 and less than or equal to 1. This set is bounded because it is contained within the range [-1, 1].

Q2. Does the intersection of sets follow associative law?

Yes, the intersection of sets follows the associative law. The associative law for the intersection of sets states that for any three sets P, Q, and R, (P ∩ Q) ∩ R = P ∩ (Q ∩ R).

Q3. What are Open sets?

An open set is a set that does not contain its limit points. For example, the set of all real numbers greater than 0 is an open set, because, for every point x in this set, we can find an open interval (x - ε, x + ε) containing x and entirely contained in the set, for some positive ε.