Introduction

To move an object or stop a moving object, some sort of effort is required in real life. This effort is generally provided in the form of a force whose effect may or may not be visible to the naked eye. As a result of the application of such a force, an object can get displaced by a certain amount and this displacement is the phenomenon of work.

In physics, work is a quantity that is precisely defined in terms of the force applied and the displacement that occurs as a result. We will discuss it in detail in this article.

Work and Energy - Overview

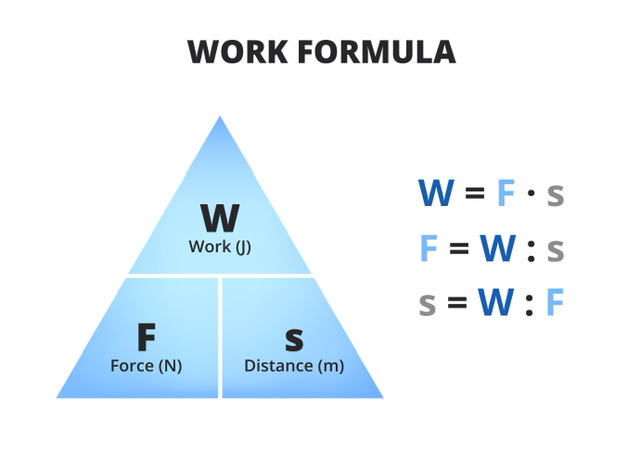
Work is defined as the product of the displacement of an object and the component of the force causing said displacement in the direction of displacement. That is,

Energy, on the other hand, is a measure of the capacity to do work and thus, any sort of work requires energy, which can appear in a large number of forms. The units of both of these quantities are the same.

What do Work and Energy Mean?

Suppose that a force F acts on an object and as a result, the object is displaced by an amount d. The work done in such a scenario is defined as the dot product of these two quantities. That is,

Energy is a physical quantity that is closely related to work. To do work, we require energy input in some form. For instance, when we lift up an object, we do work on it against the gravitational force and to do so, we provide mechanical energy via our hands.

When is Work done?

Physically, work is done only when the object gets displaced in a direction that is not perpendicular to the direction of force application. Thus, if we push a very heavy object and are unable to move it, we will get tired but physically, our work will be zero. Similarly, if the force applied is in the vertical direction and the object is moving in a horizontal direction, the work done against this force will be zero.

Example of Work done

Q. Suppose an object of mass 2 kg falls from a height of 5 m to the ground. Calculate the work done by gravitational force by neglecting air resistance and taking g = 10 ms-2 .

An object falling on the land

We know that the force of gravity acting on the body is given by F=mg=210 =20 N. To calculate the work done, we use the formula

Here, since the force and displacement are in the same direction, =1 and thus, we have:

Thus, the gravitational force does 100 J of work on the object.

What is Energy?

Energy measures how much an object is capable of doing work. If an object carries a large amount of energy, it can perform a larger amount of work as compared to an object carrying less energy. Since energy remains conserved, all the forms of energy that an object has get added up and can be used to do work.

Types of Energy

Energy is classified into a large number of types, with the most common examples being sound energy, heat energy, light energy, etc. The form of energy that is related to movement is known as mechanical energy and it is further classified into the following types:

Kinetic Energy

• This is energy related to the motion of the object. An object moving faster has a higher kinetic energy than a slower object.

• An object at rest carries no kinetic energy.

• Kinetic energy measures the amount of work that has been done to bring an object into motion.

• Mathematically,

Potential Energy

• Potential energy is related to an object’s position and composition with respect to its surroundings. For instance, a charged particle in an electric field has a potential energy depending on the strength of the field at that point. Similarly, objects in a gravitational field carry gravitational potential energy.

• The potential energy of an object depends on its position and composition with respect to its surroundings. Because the various forces acting on an object depend on its position and composition. 

• Mathematically,

The Work-Energy Principle

The work-energy theorem or work-energy principle proves the equivalence of work and energy. The most common example of this theorem relates kinetic energy to work done. If an object is moving with a kinetic energy of 10 J, that means 10 J of work was done to get it to start moving. Let us prove it:

Suppose that an object of mass m is moving on a frictionless surface due to a constant force F in the same direction. Then, the work done by the force to move it by a distance s is given as:

Here, is the change in kinetic energy of the object. Thus, we arrive at the conclusion that , which is the mathematical statement of the work-energy theorem.

Difference between Work and Energy

Summary

In layman’s terms, any sort of activity may be termed as work but in physics, it is related to the displacement of an object as a result of the application of some force in the direction of said displacement. If the object does not move or if its movement is in a perpendicular direction, no work is said to have been done. Energy measures the capacity to do work and the two quantities are related via the work-energy theorem.

Frequently Asked Questions

1. Explain kilowatt hour (kwh).

The kilowatt-hour is a unit of energy that is commonly used to measure the amount of electrical energy supplied commercially to homes. It is also known as one unit of energy and is numerically equivalent to using a 1000 W power source for one hour.

2. What is torque?

Torque, or moment of force, is the rotational analogue of force and is mathematically defined as the cross-product of force and distance. It is measured in Nm.

3. What is electric power?

Electric power measures the amount of work done or the electric energy consumed in unit time. In electrical circuits, it is given by the product of voltage and current. That is,

P=VI

The SI unit of power is ‘Watt’.

4. Prove that an object has finite velocity and finite acceleration

Velocity is related to the kinetic energy of an object and acceleration leads to an object gaining velocity. If the velocity of a body were to become infinite, that would imply that it had infinite energy, which is simply not possible.

5. What is weight?

The weight of an object is the force acting on it due to the gravitational field of a planet. Thus, an object carrying the same mass can have different weights on different planets since each planet has a different value of acceleration due to gravity.